Ever find yourself tangled in geometry like you’re trying to untangle a pair of headphones? Well, you’re not alone. Proving that triangle ABC is similar to triangle DEC using similarity transformations may seem daunting, but it’s actually more straightforward than it looks. In this text, we will break down the mystery of similarity transformations and the ideal diagrams to use, so you can solve these puzzles with ease and confidence. Let’s immerse.
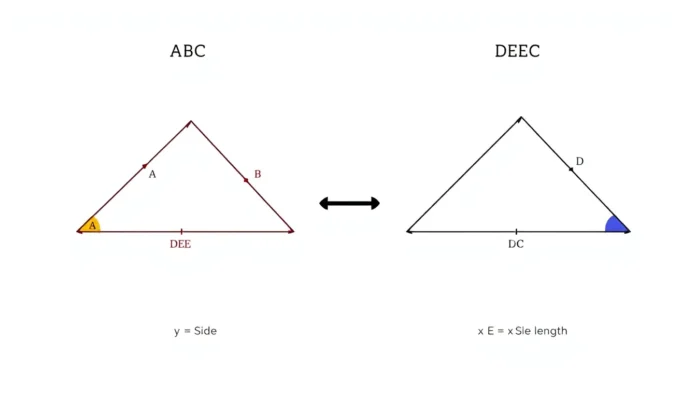
which diagram could be used to prove △abc ~ △dec using similarity transformations?
To grasp why △ABC is similar to △DEC, one must first understand similarity transformations. Simply put, similarity transformations allow you to manipulate shapes, think scaling, translating and rotating, while maintaining their essential characteristics, such as angles and proportional sides.
When triangles share similar angles and proportional sides, they can be classified as similar. This means that their shapes are identical, even if their sizes differ. In practical terms, this is crucial for solving real-world problems in architecture and engineering, where obtaining accurate measurements is everything.
Types of Similarity Transformations
There are three primary types of similarity transformations:
- Translation: This involves moving the entire triangle from one location to another without altering its shape or size. If point A moves to point A’
- Rotation: Here, the triangle is turned around a specific point, altering its orientation but not its size or shape. A rotation around point A might lead to triangle ABC occupying a new position without changing its dimensions.
- Reflection: In this method, the triangle is flipped across a line of symmetry. While the triangle’s size remains unchanged, its position may differ, allowing for unique visual presentations of the same geometric figure.
These transformations are fundamental for demonstrating similarity between triangles, as they can manipulate one triangle into the shape of another.
Analyzing △ABC and △DEC
To prove that △ABC is similar to △DEC, one needs to take a closer look at the two triangles. Several aspects come into play:
Applying Theorems of Similarity
Understanding theorems such as the Angle-Angle (AA) criterion is imperative. If two angles of one triangle are equal to two angles of another triangle, the triangles are considered similar.
Identifying Corresponding Angles
When examining triangles, corresponding angles are crucial for comparison. By marking the angles of both △ABC and △DEC, he can find instances of equal angles. For instance, if angle A equals angle D and angle B equals angle E, one can safely assert that the corresponding angles are equal.
Determining Proportional Sides
Next, it’s vital to ascertain that the sides are in proportion. The ratio of side lengths must remain consistent when comparing both triangles. If side AB is twice the length of side DE, and so forth, then the sides can be framed in equal proporitons.
Visualizing The Transformations
Visual representation offers a clearer understanding of geometric principles. Let’s explore how diagrams can help the proof of similarity:
Choosing The Right Diagram
The right diagram is imperative. When preparing a diagram, ensure it clearly illustrates △ABC and △DEC, perhaps even using color coding for angles and sides. Labeled diagrams allow for immediate comparisons, making patterns and relationships much easier to spot.
Examples of Effective Diagrams
Diagrams that feature corresponding angles clearly marked and side lengths written out will provide a solid foundation for visualizing similarity.
Consider creating a side-by-side illustration of both triangles with lines extending from the vertices to illustrate proportions. These visual cues serve as powerful reminders of the relationships between the triangles.